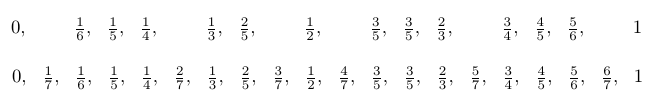打率で算数を学ぶ!~「珍しい」打率って何のこと?~
球場で野球観戦中、今でこそ好きなときに簡単にデータを調べられるようになりましたが、一昔前まではスコアボードくらいしか頼れる数字はありませんでした。NPBの試合では、打席に立っている打者の打率・本塁打・打点が表示されてきましたが、チームの得点や安打数、球速等も含めて電光掲示板で唯一 割合を表している打率に、幼き頃の私の心は躍らされたものです。打席前後の打率の変化を見ては、この選手は何打数何安打なのかの計算に頭をはりめぐらせていました。
今回は、この打率と、打率を小数第4位で四捨五入した値(以下「打率表示」とよぶ)について調べてみることにします。
「よくある」打率、「珍しい」打率
そもそも、この打率表示は何種類あるでしょうか。理論上は .000, .001, ......, .999 の1000 種類ありますが、たとえば .001 になるのはどんなときか考えてみましょう。四捨五入して 0.001 になるということは真値は 0.0005 以上 0.0015 未満であったはずです。これを満たす場合の最小の分母を計算すると、667 (667 打数 1安打のときに 1 ÷ 667 = 0.0014992…… )となります。年間最多打数記録は広瀬叔功('63 年・南海)の 626 打数ですので、年間打率に関して .001 を収めるのは非常に困難です。仮に 667 打数に達したとしても、それだけ機会の与えられる打者が 1 安打しかしていないことはありえませんね。
左図 1 は、1936 ~ 2014 年の年間打率('37, '38 年は 2 季。シーズン中の移籍選手はリーグごとに集計)の打率表示の分布を表した棒グラフです。年間 1 打数以上立った全打者を対象にし、.000 は非常に多いため除外してあります。.000 は 2 番目に多い .250 の実に 7 倍近くもの人数がいました。
.059~.370 まではすべて該当者がいましたが、決してなだらかな分布ではありません。純粋に能力として残しやすい成績( 2 ~ 3 割)にプラスして、「分数としての現れやすさ」が如実に表れていることがわかるでしょう。具体的には、
.250 → 1/4 = 0.25
.200 → 1/5 = 0.2
.333 → 1/3 = 0.33333……
.167 → 1/6 = 0.16666……
.500 → 1/2 = 0.5
などの、分母の小さい「簡単な分数」の打率表示においてピークが存在します。
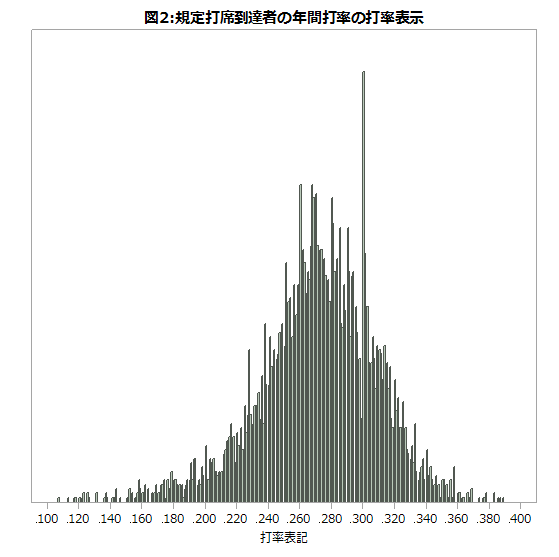
左図 2 は対象を規定打席到達者にしぼったグラフです。最頻値は .300 と、やはり分母が小さい 3/10 で表せるものの、全打者と比べ分母(打数)が大きくなるために上述の傾向はかなり薄れています。規定打席数は年度によって異なりますが、多くは400超。分母がこの程度あれば、おおよそ連続量として扱えるとも言えるでしょう。
あくまでも個人の年間打率に限りますが、打率表示の種類は391種類、規定打席到達者では235種類ありました。
.249 と .250 と .251
逆に、図 1, 2 共に周りと比べて少なめなのは .249, .299, .221, .199 などです。0 に近かった .001 が表れないのと同様に、これらは分母の小さい「簡単な分数」に近く、比較的大きな分母でしか表せない性質があるからです。たとえば .249 は 169 打数 42 安打の 0.24852…… が最小打数での達成となります。
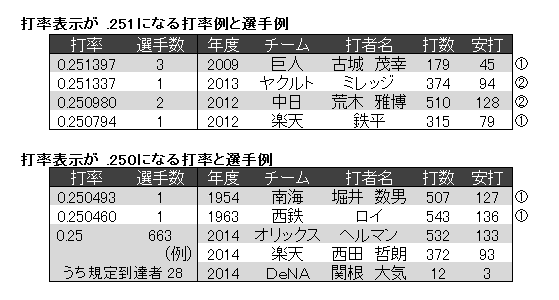
同じ打率表示の中でも、四捨五入する前の打率が異なることはよくあります。.251 はなんと 61 種類もの打率が該当していました。そのうち1人を除く全員が、
①あと 1 打数凡退したら打率がぴったり 1/4 になる場合
②あと 2 打数凡退したら打率がぴったり 1/4 になる場合
のいずれかに該当していました。
.251 がバリエーションに富んでいる一方で、お隣の .250 は 3 種類の打率しかありませんでした。.000 の次に多かった人気の打率表示ですが、.250 を見たらぴったり 1/4 だと思ってしまってほぼ正解ということになります。
3忽差のニアミス、6糸差の首位打者争い
前節で、打率表示は同じだが異なる打率について観てきましたが、もっともっと細かい部分まで着目していきましょう。
さて、最も近い、近いけれど等しくはない「ニアミス」の打率は一体いくつでしょうか。
1948 年の飯田徳治(南海)が
532 打数 149 安打で打率 0.280075……
2007 年の北川博敏(オリックス)が
557 打数 156 安打で打率 0.280071……
実に 0.000003 差、「0 割 0 分 0 厘 0 毛 0 糸 3 忽 3 微 7 繊 」差でした。国鉄・サンケイ・南海監督も務めた飯田と、球史に残る一振りを見せた北川。温厚な性格として知られる両者が半世紀の時を経て 3 忽差の打率を残しました。
この 3 忽差について分数で計算してみると、右のようになります。2 つの分数の差を計算するとき、通分によって分子が 1 になる場合、それら 2 つは「隣り合う分数」とよばれています。
同一年度同一リーグでの差が最小となったのは 2002 年の福浦和也(ロッテ・567 打数 172 安打 0.303350……)とフェルナンデス(ロッテ・478 打数 145 安打 0.303347……)の 3 忽 6 微 9 繊差。小数第 6 桁まで書かないと区別できないことになりますが、新聞表記はどうなっていたのか気になります。ちなみに昨年は大和と黒羽根利規の1糸5忽4微差でした。
また、首位打者争いで史上最も僅差の決着となったのは 1976 年の谷沢健一(中日・496 打数 176 安打 0.35483……)と張本勲(巨人・513 打数 182 安打 0.35477……)の 6 糸 2 忽 9 微差。8 度目の首位打者を逃した張本はこれ以降、タイトルをとれずに引退しています。
なお、これら 4 組の打率はすべて、隣り合っていました。
野球から学べる算数・数学
隣り合った分数が並ぶ数列として、Farey数列とよばれる数列があります。0~1の範囲の分数(約分したもの)を小さい順に並べた数列です。例として、分母が6以下、7以下の分数に限定したものを下にのせておきます。打率もこんな要領で並べていけばおもしろいのではないか?――私が初めてFarey数列に出会ったとき、打率でわくわくしたかつての記憶がふとよみがえってきたのを 思い出します。
上段(分母が 6 以下)から下段(分母が 7 以下)を作成するとき、1/7 ~ 6/7 をどこかに差し込む必要があります。たとえば 3/7 はどこにあるかとっさに判断できるでしょうか。 2/5 < 3/7 < 1/2 という大小関係を通分せずに説明する方法があります。3/7はその前後の 2/5, 1/2 を分子同士、分母同士で足した
| になっていることを利用するのです(実は、どの3連続数についても同様の性質が成り立ち |
ます)。
これらの分数を打率に置き直してみます。「7 打数 3 安打」を「5 打数 2 安打したあと 2 打数 1 安打した」とみなすことで、5 打数 2 安打と 2 打数 1 安打の間の成績だとわかります。それによって 3/7 は 2/5 と 1/2 の間の値である、と納得できた野球好きな少年もいます。
このように天秤算、加重平均の理解に打率が一役買うなんてこともあるのです。
野球の名鑑、成績表、スコアボードには様々な数字があふれています。セイバーメトリクスのような統計学的な手法での数字の楽しみ方もありますが、多くの教材も隠されています。野球を通じて算数を身につけ、そして算数を通じて野球がより身近になっていく。そんな教育があってもよいのではないかと思います。