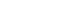機械学習を用いてセンバツ出場校を予想する
予想の手順
今回の目的は2015年秋季地区大会に出場した各校のデータをもとに、それぞれの学校が今年の選抜大会に選出されるか否かを判別することです。今回は、次のような手順で選抜出場校を予想します。
①秋季大会の結果データをもとにその学校が選抜大会に選出されるか否かを判別する判別器を作成する。
②2006年から2015年までの選抜大会の選考結果と各年の前年(2005年から2014年まで)の秋季大会結果のデータを用いて、判別器が秋季大会のデータから、過去10年分の秋季大会出場校を選抜大会に選出されるか否か、ある程度正しく判定できるようになるまで繰り返し学習をおこなわせる。
③学習を終え選抜に選出されるか否かをある程度正しく判別できるようになった判別器に2015年秋季大会の各校の結果を入力し、その学校が選抜に選出されるか否かを予想させる。
2016年近畿地区選抜出場校予想
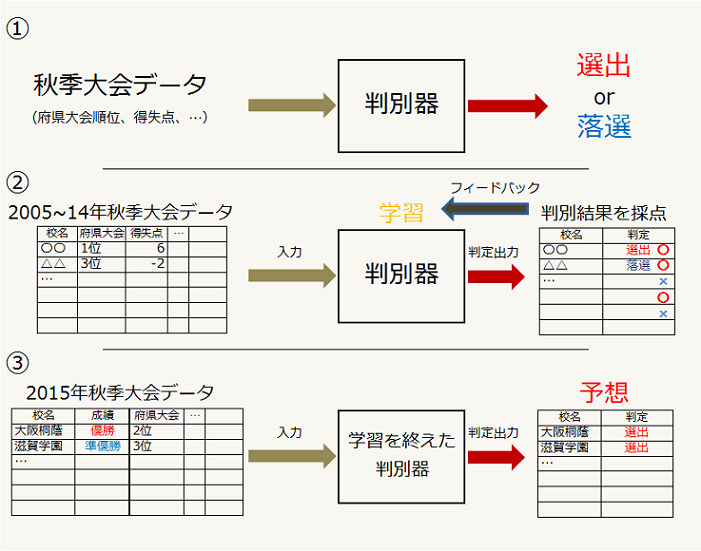
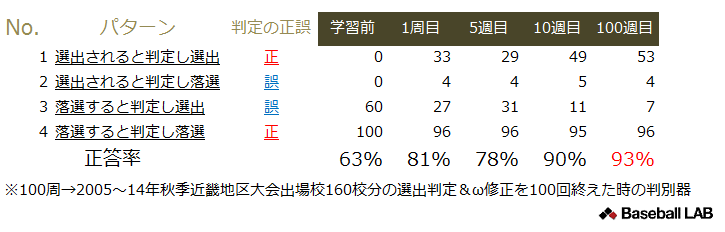
判別に使用するデータや学習過程などの詳細は後々説明することとし、先に学習を終えた判別器を使用して予想をおこなった結果を右表に示しておきます。予想には学習を終え2005年から2014年までの秋季近畿地区大会出場校を、秋季大会の結果をもとに翌年の選抜に出場するか否か93%の確率で正しく判定することができるようになった判別器を用いています。
近畿地区に与えられている出場枠は6枠。2015年秋季大会に出場した16校のうち判別器が「選出」と予想を出した学校は大阪桐蔭(近畿大会優勝・大阪2位)、滋賀学園(同準優勝・滋賀3位)、龍谷大平安(同ベスト4・京都1位)、明石商(同ベスト4・兵庫1位)、智弁学園(同ベスト8・奈良1位)、市和歌山(同ベスト8・和歌山1位)の計6校でした。
この判別器は判別をおこなう学校の秋季大会の結果データのみを見て選出・落選を判定します。秋季大会に出場した16校の判定を行う過程で他校の判定結果は考慮しないため、6つの出場枠に対して7、8校に選出の判定を出すことや、逆に選出枠よりも少ない数しか選出の判定を出さない可能性もありましたが今回は出場枠数と同じ6校に対して選出の判定が出ました。
判別器の学習手順
ここからは判別器の概要と、今回おこなわせた学習について簡単に説明したいとおもいます。
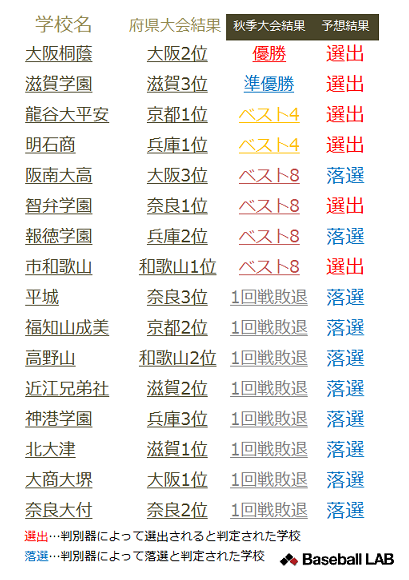
〇判別器の概要
先程の予想に使用した判別器は入力として秋季大会の結果データを受け取り、それをもとに選出または落選という判別結果を出力します。判別器の選出・落選は各入力信号X1,X2,…Xiとそれぞれの入力値に対して設定した重みω1,ω2,…ωiを掛けあわせた和をもとに決定します。例えばX1ω1+ X2ω2+…+Xiωiの値が20以上なら選出、19以下なら落選といった具合に、あらかじめ判定基準を決めておきます。この選出・落選の基準値と各入力値に掛けあわされるω1,ω2,…ωiの値を適当に設定してから学習を開始します。
〇学習の流れ
①実際の過去の秋季大会データでX1ω1+ X2ω2+…+Xiωiを計算しその学校が選出か落選か判定を行わせる。
②判定を行った学校が実際に選出されたか否かを確認し、選出・落選を正しく判定できていた場合、そのまま次の学校の判定をおこなう。正しく判定できていない場合、ω1,ω2,…ωiの重みを現在の判定が出にくくなるように調整(更新)したのち次の学校の判定をおこなう。
③ ②を全てのデータに対して反復しておこない(近畿地区であれば過去10年間述べ160校のデータに対して複数回②をおこなわせる)、全く誤判定がなくなるか各ωの値がある程度収束してきたところで学習を終了させる。
このようにして各ωの値を更新していくことで、判別器はより多くの入力データに対して正しい判定を下せるようになって行きます。
実はこの「ωの値を更新していく」という行為が今回の判別器の学習にあたります。この説明だけでは少しイメージが湧きにくいかと思いますので次の章でグラフを用いて考えてみましょう。
学習していくとは
先程「ωの値を更新していく」という行為が判別器の学習にあたると書きましたが、ωの値を更新していくことで何が起こっているのでしょうか。判別器に入力する変数を2つにして考えてみましょう。今回は例として「秋季大会の成績」と「秋季大会最終戦の得点」を入力する2つの変数として使用することにします。
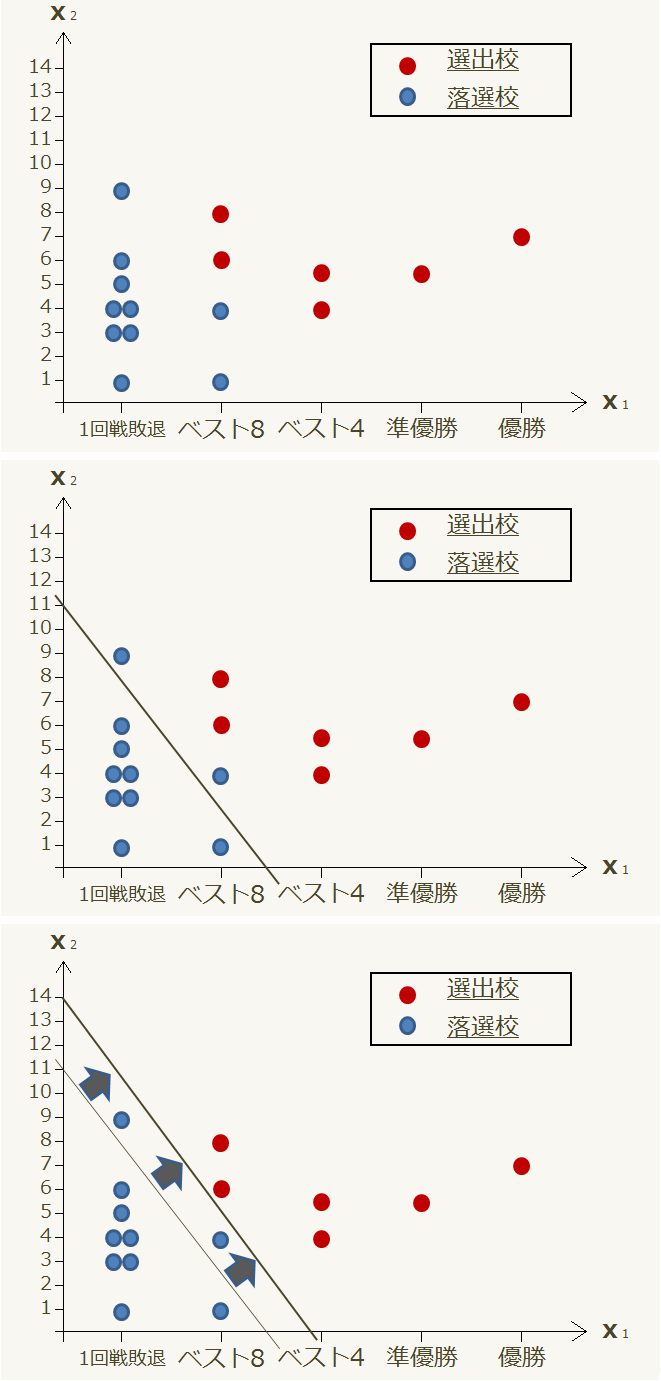
過去の秋季大会出場校の成績(X1)と各チームの最終戦の得点(X2)をプロットし、それぞれのチームが選出されたか否か調べた所、グラフのような結果が得られたとします。このグラフに適当に一本の直線を引いてみましょう。
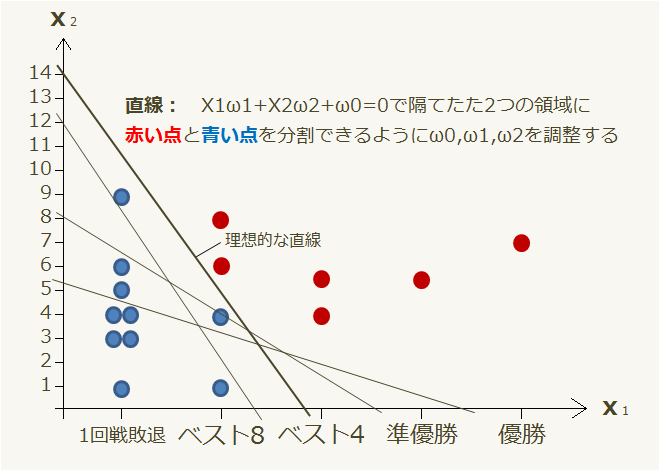
今、この直線の上側には選出校を示す赤い点が6つと落選校を示す青い点が2つ、下側には落選校を示す青い点が8つあることが分かります。この直線を少し移動させてみましょう。
このように直線の傾きと位置を修正することで、赤い点と青い点を直線の上側と下側の領域で分けることが出来ます。